|
Below are some research articles I have written or co-authored. The focus
is on Markov Processes and their applications to large scale scientific computation problems.
To illustrate some of these ideas, I have also written several Markov Chain
demonstration applets in Java.
-
Web graph compression in MarkovPR 1.1
(2002)
-
abstract:
These notes describe the results of some investigations into
reducing the memory requirements of the MarkovPR 1.0 software
for storing, and simulating from, massive web graphs. The
statistics which illustrate our results are based upon the
First Google Programming Contest dataset. Many of the techniques
described here have been implemented in the new version, MarkovPR 1.1.
-
source code (licensed under GPL): markovpr-1.1.tar.bz2
-
 ripcompress.ps.gz ripcompress.ps.gz
 ripcompress.pdf ripcompress.pdf
-
Markovian page ranking distributions: some theory and simulations
(2002)
-
abstract:
We discuss some simple theoretical properties of web page ranking
distributions, including PageRank (Brin and Page, 1998), which are
based on uniformly ergodic Markov chains. We also propose a
modification of PageRank with reduces the bias for older documents,
and discuss details of our simulation programs.
-
source code (licensed under GPL): markovpr-1.01.tar.gz
-
 googlerip.ps.gz googlerip.ps.gz
 googlerip.pdf googlerip.pdf
-
Some directions in Perfect Simulation
(2000)
-
abstract:
Presentation given at the First European Conference on Spatial Statistics, Ambleside (17-22 september, 2000).
The slides here have been slightly modified for web viewing. You can find the
LaTeX source code and instructions
for creating the slides here.
-
 ambleside2.pdf ambleside2.pdf
-
A note on geometric ergodicity and floating-point roundoff error
(2000)
-
coauthored with
Gareth Roberts and
Jeff Rosenthal
-
abstract:
We consider the extent to which Markov chain convergence properties are affected by
the presence of computer floating-point roundoff error. Both geometric ergodicity and
polynomial ergodicity are considered. This paper extends previous work of Roberts,
Rosenthal and Schwartz (1998); connections between that work and the present paper
are discussed.
-
 glj8.ps.gz glj8.ps.gz
 glj8.pdf glj8.pdf
-
Catalytic perfect simulation
(2000)
-
coauthored with
Gareth Roberts
-
abstract:
We introduce a methodology for perfect simulation using so called catalysts to modify
random fields. Our methodology builds on a number of ideas previously introduced by
Breyer and Roberts (1999), by Murdoch (1999), and by Wilson (1999). We illustrate our
techniques by simulating two examples of Bayesian posterior distributions.
-
 simulations5.ps.gz simulations5.ps.gz
 simulations5.pdf simulations5.pdf
-
slides also available:
 catalytic_slides.ps.gz catalytic_slides.ps.gz
 catalytic_slides.pdf catalytic_slides.pdf
-
Some multi-step coupling constructions for Markov chains
(2000)
-
coauthored with
Gareth Roberts
-
abstract:
We describe some old and new methods for coupling the flow of a discrete time Markov
chain, provided its transition function is known. Examples including Hastings-Metropolis
and Gibbs samplers are given.
-
 multistep.ps.gz multistep.ps.gz
 multistep.pdf multistep.pdf
-
On the approximation of certain probability measures by a set of points
(2000)
-
abstract:
In this paper we describe a framework for the comparison of a finite set of points with a
probability measure if the latter belongs to a simple class. The measure of closeness
chosen quantifies the degree of agreement obtained when a prescribed collection of test
functions is simultaneously integrated with respect to the given probability measure, and
the set of points (identified with a sum of point masses). No specific assumptions are
made about the provenance of the point set, although our results have a clear application
to certain Markov chain Monte Carlo integration problems.
-
 hypo.ps.gz hypo.ps.gz
 hypo.pdf hypo.pdf
-
Convergence of simulated annealing using Foster-Lyapunov criteria
(2000)
-
coauthored with
Christophe Andrieu and
Arnaud Doucet
-
abstract:
Simulated annealing is a popular and much studied method for maximizing functions on
finite or compact spaces. For noncompact state spaces, the method is still sound, but
convergence results are scarce. We show here how to prove convergence in such cases,
for Markov chains satisfying suitable drift and minorization conditions.
-
 ANNEAL.ps.gz ANNEAL.ps.gz
 ANNEAL.pdf ANNEAL.pdf
-
Efficient Monte Carlo for neural networks with Langevin samplers
(1999)
-
coauthored with
Mauro Piccioni and
Sergio Scarlatti
-
abstract:
We consider the task of simulating efficiently from the posterior distribution over weight
space of a feed-forward neural network using a Langevin-Metropolis sampler, given a
finite data set. It is shown that as the number
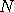 of hidden neurons increase, the proposal
variance must scale as of hidden neurons increase, the proposal
variance must scale as 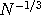 in order to get convergence of the underlying discretized
diffusions. This generalizes previous results of Roberts and Rosenthal (1998) for the i.i.d.
case, shows robustness of their analysis, and also has practical applications. in order to get convergence of the underlying discretized
diffusions. This generalizes previous results of Roberts and Rosenthal (1998) for the i.i.d.
case, shows robustness of their analysis, and also has practical applications.
-
 neural14.ps.gz neural14.ps.gz
 neural14.pdf neural14.pdf
-
A new method for coupling random fields
(1999)
-
coauthored with
Gareth Roberts
-
abstract:
Given a Markov chain, a stochastic flow which simultaneously constructs sample paths
started at each possible initial value can be constructed as a composition of random
fields. In this paper, we describe a method for coupling flows by modifying an arbitrary
field (consistent with the Markov chain of interest) by an independence Metropolis
Hastings iteration. We show that the resulting stochastic flow has many desirable
coalescence properties, regardless of the form of the original flow.
-
 fcoupler.ps.gz fcoupler.ps.gz
 fcoupler.pdf fcoupler.pdf
-
slides also available:
 poster99-2.ps.gz poster99-2.ps.gz
 poster99-2.pdf poster99-2.pdf
-
Quasistationarity and the relative entropy of probability measures
(1999)
-
abstract:
Consider a Markov process
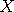 with finite lifetime. In this paper, we derive sufficient
conditions for the convergence of the law of with finite lifetime. In this paper, we derive sufficient
conditions for the convergence of the law of 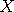 , conditioned on longer and longer lifetimes,
using information theoretic techniques. , conditioned on longer and longer lifetimes,
using information theoretic techniques.
-
 quasism.ps.gz quasism.ps.gz
 quasism.pdf quasism.pdf
-
From Metropolis to diffusions: Gibbs states and optimal scaling
(1998)
-
coauthored with
Gareth Roberts
-
abstract:
This paper investigates the behaviour of the random walk Metropolis algorithm in high
dimensional problems. Here we concentrate on the case where the components in the
target density is a spatially homogeneous Gibbs distribution with finite range. The
performance of the algorithm is strongly linked to the presence or absence of phase
transition for the Gibbs distribution; the convergence time being approximately linear in
dimension for problems where phase transition is not present. Related to this, there is an
optimal way to scale the variance of the proposal distribution in order to maximise the
speed of convergence of the algorithm. This turns out to involve scaling the variance of
the proposal as the reciprocal of dimension (at least in the phase transition free case).
Moreover the actual optimal scaling can be characterised in terms of the overall
acceptance rate of the algorithm, the maximising value being 0.234, the value as
predicted by studies on simpler classes of target density. The results are proved in the
framework of a weak convergence result, which shows that the algorithm actually
behaves like an infinite dimensional diffusion process in high dimensions.
-
 scaling.ps.gz scaling.ps.gz
 scaling.pdf scaling.pdf
-
Yaglom limits via compactifications
(1998)
-
abstract:
Consider a Markov process
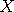 with finite lifetime. In this paper, we derive sufficient
conditions for the existence of a Yaglom limit, or limiting conditional distribution for with finite lifetime. In this paper, we derive sufficient
conditions for the existence of a Yaglom limit, or limiting conditional distribution for 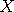 . .
-
 qmart2.ps.gz qmart2.ps.gz
 qmart2.pdf qmart2.pdf
-
Quasistationarity and Martin boundaries: Conditioned processes
(1998)
-
abstract:
Consider a Markov process
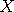 with finite lifetime with finite lifetime  . In this paper, we derive sufficient
conditions which allow the conditioning of . In this paper, we derive sufficient
conditions which allow the conditioning of 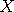 to an infinite lifetime. This is accomplished
by showing the weak convergence, as to an infinite lifetime. This is accomplished
by showing the weak convergence, as 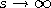 , of the laws of , of the laws of
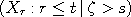 . .
-
 qmart1.ps.gz qmart1.ps.gz
 qmart1.pdf qmart1.pdf
-
On a parabolic Harnack inequality for Markov chains
(1998)
-
abstract:
For continuous time Markov chains on a countable state space, we derive a parabolic
Harnack inequality using probabilistic methods. We derive some consequences of this
inequality for the compactness of parabolic (\ie spacetime harmonic) functions of the
process.
-
 parabolic.ps.gz parabolic.ps.gz
 parabolic.pdf parabolic.pdf
-
A quasi-ergodic theorem for evanescent processes
(1997)
-
coauthored with
Gareth Roberts
-
abstract:
We prove a conditioned version of the ergodic theorem for Markov processes, which we
call a quasi-ergodic theorem. We also prove a convergence result for conditioned
processes as the conditioning event becomes rarer.
-
 ergo2_rev.ps.gz ergo2_rev.ps.gz
 ergo2_rev.pdf ergo2_rev.pdf
-
Quasistationarity and Conditioned Markov Processes
(1997)
-
abstract:
Ph.D. thesis.
-
 phd-thesis.ps.gz phd-thesis.ps.gz
 phd-thesis.pdf phd-thesis.pdf
-
Quasistationary theorems for diffusions in a bounded open set
(1996)
-
abstract:
Let
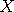 be the minimal diffusion associated with a uniformly elliptic differential operator be the minimal diffusion associated with a uniformly elliptic differential operator 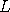 in a bounded subdomain of
in a bounded subdomain of 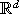 , with , with 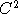 boundary. Under the only assumption that the
coefficients of boundary. Under the only assumption that the
coefficients of 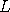 be Hölder continuous, we prove all the standard quasistationary limit
theorems (cf. Markov chain theory). Moreover, we show that the laws of be Hölder continuous, we prove all the standard quasistationary limit
theorems (cf. Markov chain theory). Moreover, we show that the laws of 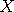 , conditioned
on explosion occuring after time , conditioned
on explosion occuring after time  , converge in total variation, as s tends to infinity, to the
law of a positive recurrent diffusion , converge in total variation, as s tends to infinity, to the
law of a positive recurrent diffusion 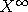 , which is related to , which is related to 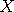 by the addition of the drift by the addition of the drift
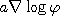 , where , where 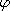 is the ground state of is the ground state of 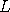 .
Previously, such results were shown only for symmetrically reversible diffusions. .
Previously, such results were shown only for symmetrically reversible diffusions.
-
 multidiffb.ps.gz multidiffb.ps.gz
 multidiffb.pdf multidiffb.pdf
-
Approximations of quasistationary distributions for Markov chains
(1996)
-
coauthored with
Andrew Hart
-
abstract:
We consider a simple and widely used method for evaluating quasistationary distributions
of continuous time Markov chains. The infinite state space is replaced by a large, but
finite approximation, which is used to evaluate a candidate distribution. We give some
conditions under which the method works, and describe some important pitfalls.
-
 approxr.ps.gz approxr.ps.gz
 approxr.pdf approxr.pdf
-
Honours project: A tutorial on stochastic calculus
(1994)
-
abstract:
Fourth year honours project report. An introduction to stochastic calculus with a detailed
bibliography.
-
 hon-thesis.ps.gz hon-thesis.ps.gz
 hon-thesis.pdf hon-thesis.pdf
|





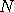 of hidden neurons increase, the proposal
variance must scale as
of hidden neurons increase, the proposal
variance must scale as 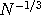 in order to get convergence of the underlying discretized
diffusions. This generalizes previous results of Roberts and Rosenthal (1998) for the i.i.d.
case, shows robustness of their analysis, and also has practical applications.
in order to get convergence of the underlying discretized
diffusions. This generalizes previous results of Roberts and Rosenthal (1998) for the i.i.d.
case, shows robustness of their analysis, and also has practical applications.
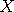 with finite lifetime. In this paper, we derive sufficient
conditions for the convergence of the law of
with finite lifetime. In this paper, we derive sufficient
conditions for the convergence of the law of  . In this paper, we derive sufficient
conditions which allow the conditioning of
. In this paper, we derive sufficient
conditions which allow the conditioning of 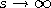 , of the laws of
, of the laws of
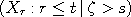 .
.
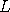 in a bounded subdomain of
in a bounded subdomain of 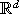 , with
, with 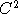 boundary. Under the only assumption that the
coefficients of
boundary. Under the only assumption that the
coefficients of  , converge in total variation, as s tends to infinity, to the
law of a positive recurrent diffusion
, converge in total variation, as s tends to infinity, to the
law of a positive recurrent diffusion 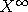 , which is related to
, which is related to 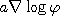 , where
, where 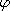 is the ground state of
is the ground state of