|
Coupling constructions for Markov chains are closely related to the study of convergence to the
stationary distribution and so called mixing times. On this page, I shall discuss briefly a universal
coupling method which applies to any Markov chain whose transition probabilities are known.
This includes all Metropolis-Hastings samplers used in practice. An accompanying paper may be
found here
(ps/pdf).
Let 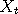 and and 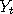 be two Markov chains with the same transition density be two Markov chains with the same transition density
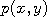 . A common way of
simulating such chains is by the rules . A common way of
simulating such chains is by the rules 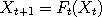 and and 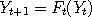 ,
where ,
where 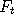 refers to some
(non unique) computer program which implements one simulation step (iteration) at time refers to some
(non unique) computer program which implements one simulation step (iteration) at time 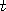 . It is
exceedingly unlikely that, for a typical . It is
exceedingly unlikely that, for a typical  , we can get , we can get 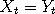 , at any time , at any time 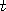 .
Why should we look for ways of simulating chains which can couple in a finite time? Theory tells
us that if we wait until two suitably chosen chains meet, then we have waited long enough for
proper mixing. More precisely, the coupling inequality says that, if the Y process is stationary,
then .
Why should we look for ways of simulating chains which can couple in a finite time? Theory tells
us that if we wait until two suitably chosen chains meet, then we have waited long enough for
proper mixing. More precisely, the coupling inequality says that, if the Y process is stationary,
then
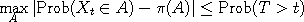
where 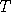 is the first time that is the first time that 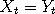 occurs, and occurs, and
 is the stationary distribution. In effect, the two
chains have lost all dependence upon their initial positions, which is useful for Markov chain
Monte Carlo. Moreover, knowing how to make Markov chains come together is a fundamental
ingredient of perfect simulation.
One easy way to construct coalescing Markov chains consists in modifying an existing transition
rule is the stationary distribution. In effect, the two
chains have lost all dependence upon their initial positions, which is useful for Markov chain
Monte Carlo. Moreover, knowing how to make Markov chains come together is a fundamental
ingredient of perfect simulation.
One easy way to construct coalescing Markov chains consists in modifying an existing transition
rule 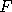 in such a way that
nearby chains have a chance of coming together in one step,
the transition density in such a way that
nearby chains have a chance of coming together in one step,
the transition density 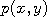 is preserved. is preserved.
Such a rule is described in the accompagnying paper
(ps/pdf),
but can also be described briefly in
the following words. At each time t, we select at random a point 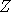 in the state space, called a
catalyst. Next, rather than update in the state space, called a
catalyst. Next, rather than update 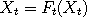 (and similarly for (and similarly for 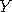 ), we let ), we let
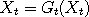 (and
similarly (and
similarly 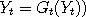 , where , where 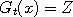 with a suitably chosen probability with a suitably chosen probability
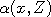 and and 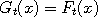 otherwise.
The right choice for a means that we do not destroy the transition probabilities,
and if both otherwise.
The right choice for a means that we do not destroy the transition probabilities,
and if both 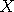 and and 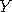 simultaneously accept the move to simultaneously accept the move to 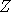 then they must meet.
The coupling method outlined above does not just work for two chains, but can be applied to as
many processes as desired simultaneously. Moreover, as many catalysts as desired can be
introduced, since the transition density is preserved every time. The applet below illustrates this in
the case when the underlying chains are Metropolized random walks with Gaussian increments
(as seen in M-H algorithms) and the catalysts are chosen uniformly in the unit square. To
distinguish the catalysts from the underlying chains, the former are surrounded by circles.
You can choose the number of catalysts as well as the number of Markov chains to couple,
together with the corresponding jump sizes denoted s. If you select zero catalysts, you see that
the chains come closer together but do not meet eventually (except due to numerical errors). If
you click once inside the image, the simulation is paused. Clicking again resumes it. then they must meet.
The coupling method outlined above does not just work for two chains, but can be applied to as
many processes as desired simultaneously. Moreover, as many catalysts as desired can be
introduced, since the transition density is preserved every time. The applet below illustrates this in
the case when the underlying chains are Metropolized random walks with Gaussian increments
(as seen in M-H algorithms) and the catalysts are chosen uniformly in the unit square. To
distinguish the catalysts from the underlying chains, the former are surrounded by circles.
You can choose the number of catalysts as well as the number of Markov chains to couple,
together with the corresponding jump sizes denoted s. If you select zero catalysts, you see that
the chains come closer together but do not meet eventually (except due to numerical errors). If
you click once inside the image, the simulation is paused. Clicking again resumes it.
An interesting question to ponder here is the following: what is the optimal number of catalysts to ensure that
all test chains coalesce in as few steps as possible? Theory tells us that it doesn't matter how many catalysts
we use, since in each case we get coalescence in a finite time. However, a bit of experimentation might convince
you that, firstly, two catalysts are better than one, and secondly, a great many catalysts just makes things worse.
This last statement can be backed up by theory, see
|


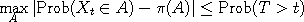



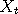 and
and 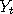 be two Markov chains with the same transition density
be two Markov chains with the same transition density
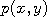 . A common way of
simulating such chains is by the rules
. A common way of
simulating such chains is by the rules 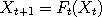 and
and 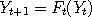 ,
where
,
where 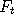 refers to some
(non unique) computer program which implements one simulation step (iteration) at time
refers to some
(non unique) computer program which implements one simulation step (iteration) at time 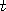 . It is
exceedingly unlikely that, for a typical
. It is
exceedingly unlikely that, for a typical 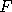 , we can get
, we can get 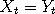 , at any time
, at any time 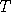 is the first time that
is the first time that  is the stationary distribution. In effect, the two
chains have lost all dependence upon their initial positions, which is useful for Markov chain
Monte Carlo. Moreover, knowing how to make Markov chains come together is a fundamental
ingredient of perfect simulation.
One easy way to construct coalescing Markov chains consists in modifying an existing transition
rule
is the stationary distribution. In effect, the two
chains have lost all dependence upon their initial positions, which is useful for Markov chain
Monte Carlo. Moreover, knowing how to make Markov chains come together is a fundamental
ingredient of perfect simulation.
One easy way to construct coalescing Markov chains consists in modifying an existing transition
rule 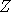 in the state space, called a
catalyst. Next, rather than update
in the state space, called a
catalyst. Next, rather than update 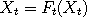 (and similarly for
(and similarly for 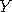 ), we let
), we let
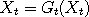 (and
similarly
(and
similarly 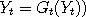 , where
, where 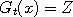 with a suitably chosen probability
with a suitably chosen probability
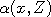 and
and 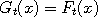 otherwise.
The right choice for a means that we do not destroy the transition probabilities,
and if both
otherwise.
The right choice for a means that we do not destroy the transition probabilities,
and if both 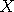 and
and