welcome/

java-mcmc/

software/

papers/

links/

I'll assume that you have run the Metropolis-Hastings applet for a while. The aim now is to see directly the effect on the transitions of "metropolizing" a proposal density. If you press the button below, a window separate from your browser should open. The window is resizable, and you may need to adjust its dimensions depending on your system configuration.

The metropolizing effect

Some of the controls of this applet should be familiar to you by now. The blue panel in the left middle of the screen is new however. It represents a graph of the metropolized transition function for the currently selected Markov chain. The diagonal line with a kink in it is a plot of the new location (y-axis) versus the old location (x-axis) after one single iteration of the Gaussian random walk Metropolis algorithm. Since each and every iteration is different, so is the corresponding graph.

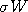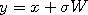The update formula can be written down explicitly as follows: at each iteration, let $x$ be the current position of the Markov chain. A Gaussian random variable $\sigma W$ is selected, which results in the proposal $y = x + \sigma W$ . When the target distribution is a Gaussian with mean 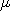$\mu$ and variance 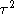$\tau^2$ , this proposal is accepted only with probability $\alpha(x,y) = \min[ 1, \exp((x -\mu)^2 - (y - \mu)^2)]$ , which gives rise to the kink. 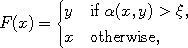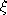The graph therefore is given by the formula $F(x) = \begin{cases} y &\text{if}\ \alpha(x,y) > \xi, \\ x &\text{otherwise}, \end{cases}$ where $\xi$ is a uniform random variable on [0,1].

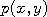The colored picture at the bottom of the window is an average of all the graphs produced. With enough iterations, this gives a representation of the transition kernel $p(x,y)$ of the selected Markov chain. The red diagonal line represents a series of point masses which account for the probability of rejecting the proposal. The picture can be reset by pressing the button labeled "Reset hist.". To see a representation of the (unmodified) proposal only, select the option "view proposal". Finally, the option "no transition graph" stops the drawing of the graph with the blue background, resulting in a faster update of the bottom picture.