 |
| welcome/ |
| java-mcmc/ |
| software/ |
| papers/ |
| links/ |
| email me |

|
Metropolis-Hastings algorithms are a class of Markov chains which are commonly used to perform large scale calculations and simulations in Physics and Statistics. The button below opens a separate window from your browser containing a demonstation of some of the most common chains which are used for this purpose. The window is resizable, and you may need to adjust its dimensions depending on your system configuration. MCMC methods in a nutshellTwo common problems which are approached via M-H algorithms are simulation and numerical integration.
The former problem consists in generating a random variable with a prescribed distribution
Moreover after that, The latter problem consists in calculating the value of a (typically complicated) integral which we write as 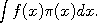
It is very rare that integrals which arise in real problems can be
evaluated explicitly in closed form, and the best one can hope for in general is an approximate
numerical value generated by a computer. The MCMC approach consists in defining as before
a Markov chain 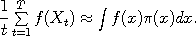
In other words, when
There are many practical problems associated with the above ideas, which to explain here is
beyond the scope of this document. Suffice to say that the main question of deciding how large to
take You can read more about MCMC methods in Bayesian statistics in the following papers (or read any of the growing number of books on the subject - see your local library for details)
For up-to-date information and the latest techniques, check out the MCMC preprint server, the McDiag Home Page and David Wilson's Perfect Simulation Home Page. Description of the appletThe applet you are seeing consists of a window which is subdivided into a number of regions. The left half of the display consists of some animated graphs, while the right half consists of some input fields and choice lists, which allow you influence what you see on the left. Choosing the target distribution
The top third of the screen consists of a graph of some distribution One of the choices in the list is the "user defined" distribution. When you select this, the box with the graph of p will be initially blank. You should see four buttons on the right, marked "New", "Accept", "Load" and "Save". Press the "New" button, and the graph should turn orange. Click somewhere in the orange box, and start dragging the mouse to draw a density. Dragging to the left erases part of the graph. Once you are happy with the distribution, press the button "Accept". The drawing screen should turn white again, and the graph you have just drawn is rescaled and displayed. To draw another, press "New" again etc. The "Load" and "Save" buttons allow you to load and save distributions which you have drawn, but for Java security reasons, these will probably not function properly over the web. Choosing the algorithm
The middle third of the screen consists of a moving red line on the left just below the graph of By clicking anywhere in the region where the red line is, you can place the chain at a new starting point and see how it evolves from there. Try selecting the Trimodal distribution in the top list box, and placing the Markov chain in each of the three bell curves.
Each of the algorithms featured in this applet functions in basically the same way. Suppose that
the random variable
propose a move to a new location 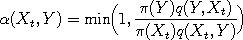 which preserves the equilibrium distribution
which preserves the equilibrium distribution  . .
The algorithms below differ only in the proposal rule. We now give brief descriptions of all the algorithms you can run. Gaussian Random Walk Metropolis
Given Much is known about this algorithm. See for example the following papers:
Uniform Random Walk Metropolis
Given Langevin
Given Some of the things known about this algorithm can be found in the following papers:
LÚvy Flight Metropolis
This is a variant of the Gaussian random walk Metropolis algorithm, where the proposal is still
Student t random walk
Like the Levy Flight Metropolis algorithm, but this time the proposal increment U[0,1] Independence Sampler
The proposal Some of the known properties of this type of algorithm can be found in the following paper:
General Independence Sampler
As above, Gareth's diffusion algorithm
This was suggested by Gareth Roberts to be a "mode hopping" algorithm. The proposal is
The idea is that whenever the chain is in a valley with low density, it should increase the variance of the jump so as to find the next mode more quickly. Gaussian Autoregressive(1)
The proposal is Hamiltonian (Hybrid) Monte Carlo
This algorithm is an example of the use of auxiliary variables, and operates a little differently
from the other algorithms above. First, we augment the number of variables which p depends on,
by taking the product of p with a standard Gaussian. This gives a two dimensional state space,
consisting of "position" and "momentum" variables. The algorithm proceeds from a value
The orange and yellow bars which you can see scrolling in step with the red path of the chain represent the current values of kinetic energy (orange) and potential energy (yellow) of the chain in phase space.
When DiagnosticsIn the lower third of the applet window, you will see on the left a box with a continuously updated histogram. On the right, you should see a plot of the estimated autocorrelation function (ACF) for the position of the chain. Just above that, there is a reset button, and two input fields which allow you to increase the number of bins in the histogram and the maximum lag used for computing the ACF. Histogram
On the left side of the window, you can see a continually updated histogram of the position of the
chain. As described earlier, for any function
A measure of the distance of the blue histogram to its theoretical limit (grey) is given by the total
variation (TV) norm, which is a number between 0 and 2. The number computed is not the total
variation distance of the law of On the histogram display, you can see also the proportion of all moves of the chain where the proposal was accepted. By setting the iteration delay on the right side to zero, the chain may be speeded up a little. Please remember that Java is an interpreted language, so these algorithms will run much faster if implemented in a language such as C. ACF plotOn top of the histogram, you can also see two vertical lines, one green and one red, which is moving. These represent respectively the location of the mean of p, and its estimate via the time averaged value of the position of the chain. Eventually, the two lines should coincide.
It is possible to measure the correlation between the successive values of the position of
It is possible to estimate the "efficiency" of the Markov chain
|



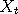 , in such a way that its equilibrium
distribution is the "target"
, in such a way that its equilibrium
distribution is the "target" 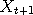 ,
, 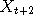 etc. it can be shown
that the distribution of
etc. it can be shown
that the distribution of 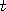 is large is close to
is large is close to 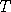 sufficiently large, the random variable
sufficiently large, the random variable
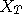 is approximately the variable we are looking for.
is approximately the variable we are looking for.
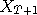 ,
, 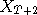 etc. are all distributed close to
etc. are all distributed close to 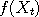 up to time
up to time 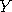 according to some prescribed rule (we must be able
to write down a probability density function
according to some prescribed rule (we must be able
to write down a probability density function 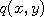 of going from
of going from 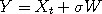 , where
, where 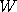 is a standard Gaussian random variable, and
is a standard Gaussian random variable, and  therefore regulates the size of the proposed jump.
therefore regulates the size of the proposed jump.
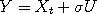 , where
, where 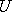 is uniformly distributed over
the range [-1,1].
is uniformly distributed over
the range [-1,1].
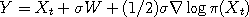 .
Unlike the Random Walk Metropolis, this algorithm uses some information about the shape of
.
Unlike the Random Walk Metropolis, this algorithm uses some information about the shape of  stable distribution.
The great French probabilist Paul LÚvy pioneered the study of these random variables.
When
stable distribution.
The great French probabilist Paul LÚvy pioneered the study of these random variables.
When 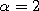 , the variable
, the variable 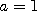 ,
,
 is, the heavier the tails of the distribution of
is, the heavier the tails of the distribution of 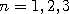 , etc. degrees of freedom.
, etc. degrees of freedom.
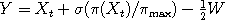 , where
, where 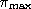 is the maximum
value of
is the maximum
value of 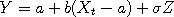 , where
, where 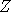 is a standard Gaussian.
This is a generalization of both the Independence Sampler and the Random Walk Metropolis chain.
If
is a standard Gaussian.
This is a generalization of both the Independence Sampler and the Random Walk Metropolis chain.
If 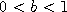 this strategy shrinks the current state toward the point a before adding
the increment
this strategy shrinks the current state toward the point a before adding
the increment 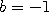 then the current state is first reflected about the
point
then the current state is first reflected about the
point  .
.
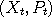 in phase space to a new value
in phase space to a new value 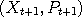 by first randomizing
by first randomizing 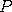 according to the
autoregressive formula
according to the
autoregressive formula 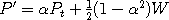 where
where 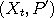 to the new value
to the new value 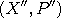 along the contour curves of the Hamiltonian
along the contour curves of the Hamiltonian 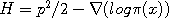 .
This last value is
accepted or rejected according to the usual Metropolis-Hastings rule.
.
This last value is
accepted or rejected according to the usual Metropolis-Hastings rule.
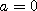 , the algorithm behaves like the Langevin algorithm.
, the algorithm behaves like the Langevin algorithm.
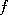 , the time averaged value of
, the time averaged value of 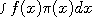 . If we pick a point
. If we pick a point 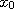 and let
and let
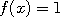 for all
for all  in a narrow bin around the
value
in a narrow bin around the
value 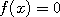 otherwise, we can get an estimate of
otherwise, we can get an estimate of 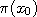 as the bin gets ever narrower. The theoretical value of this estimate is shown by the height of the grey bins, whereas
the blue bins represent the current computed average. As the number of iterations increases,
the blue bins converge to the corresponding grey bins.
as the bin gets ever narrower. The theoretical value of this estimate is shown by the height of the grey bins, whereas
the blue bins represent the current computed average. As the number of iterations increases,
the blue bins converge to the corresponding grey bins.
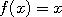 , which
estimates the mean of
, which
estimates the mean of 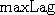 is the maximum
autocorrelation lag plotted on screen:
is the maximum
autocorrelation lag plotted on screen:
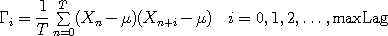 and then
and then ![\text{efficiency} = [ 1 + 2 \sum_i \Gamma_i/\Gamma_0 ]^{-1}](tex/classic-51.gif) .
.